Please feel free to read the report
Background
In 2007, authors Shai Avidan and Ariel Shamir introduced the seam carving algorithm for content-aware image resizing. Normally, resizing images may become distored or warped due to the aspect ratio not being preserved and may also lose information when they are cropped. The seam carving algorithm aims to preserve the original image content while resizing for a more adaptable resizing experience. To achieve this, the algorithm calculates energy values for all the pixels in an image based on their importance. Then a "seam" is identified by finding the lowest energy-connected pixels in either the vertical or horizontal direction to then be "carved out". Through the repetition of carving seams will reduce the image size while simultaneously preserving content that is deemed important to maintain a balance between image content and carved seams.
The motivation behind my work stems from this idea of resizing and preserving content. As mentioned before, the seam carving algorithm was introduced as an image resizing technique. But what if this algorithm can be applied on audio? Seam carving is performed on an image in its 2d array form. However, audio can also be represented in a 2d array format as a complex-valued matrix. In theory the algorithm may now be applied to the matrix where both the vertical and horizontal components can be carved. Notice that carving in the vertical context translates to the time domain while the horizontal context translates to the frequency domain. Example audio samples are below in the "Examples" section.
Strategy
I had previously implemented the seam carving algorithm using Dijkstra's algorithm in one of my classes at UW. Although this approach produces the desired results, its time complexity is not satisfactory for large-scale projects. For this to be applicable on projects that require heavy computational work, I thought a dynamic programming approach would be faster since I ultimately am searching the shortest path from the "top to bottom" in the 2d array. The code can be found on my github and it was optimized with numba.
The audio files that I worked with are in the format of .wav. The idea was to convert the .wav files to the time domain and apply the Short-Time Fourier Transform to convert to the frequency domain. With this, the magnitude and phase could be extracted and used for seam carving. The seam carving algorithm is ran on the magnitude array where the smallest-weight paths are chosen to be deleted. Simultaneously, the same seams are deleted in phase array. Once the chosen amount of seams are carved, the magnitude and phase arrays are multiplied (mag*e^(j*phase)) to reconstruct the complex spectrogram. The Inverse Short-Time Fourier Transform creates the resulting time domain array to be converted back to a .wav file. This algorithm can be used on various formats audio as long as there is a 2d array to work with. For example, some other variations that I tested on was the power density spectrogram, power log spectrogram, and the MFCC representation for just the image of the spectrogram.
The implementation varied whether the seams were carved in the time or frequency domain. If the seams were carved in the time domain, the resulting 2d array was left shortened and normally transformed back into the time domain. If the seams were carved in the frequency domain, the resulting 2d array was padded with zeros at the end equal to the amount that was carved out. This was done to preserve the original shape because of the way librosa's istft function works**.
Examples
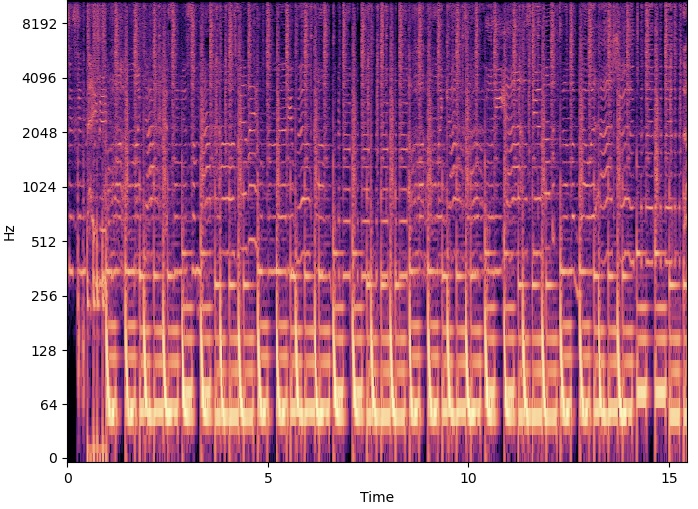
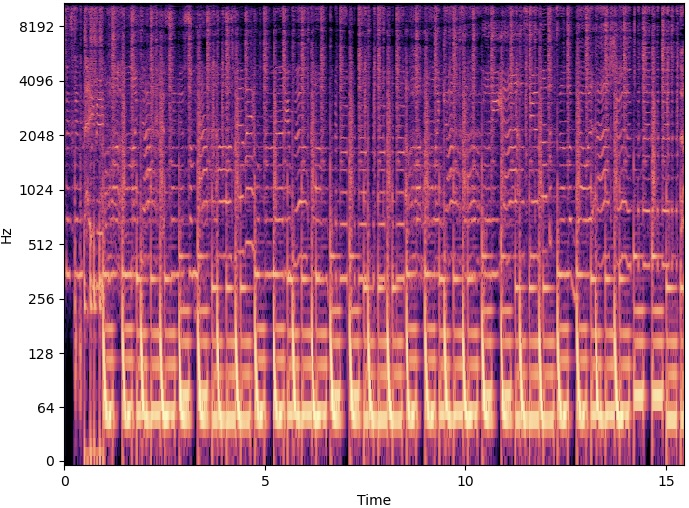
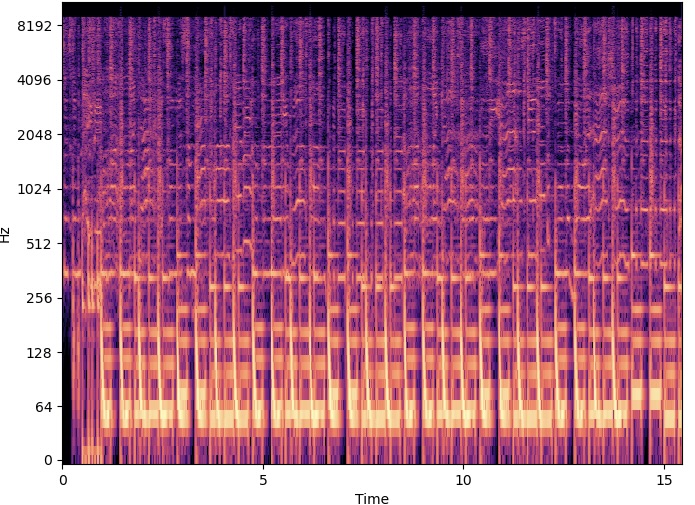
Carving in the Frequency Domain:
| Original | 400 Seams Carved | 600 Seams Carved | |
|---|---|---|---|
|
|
|
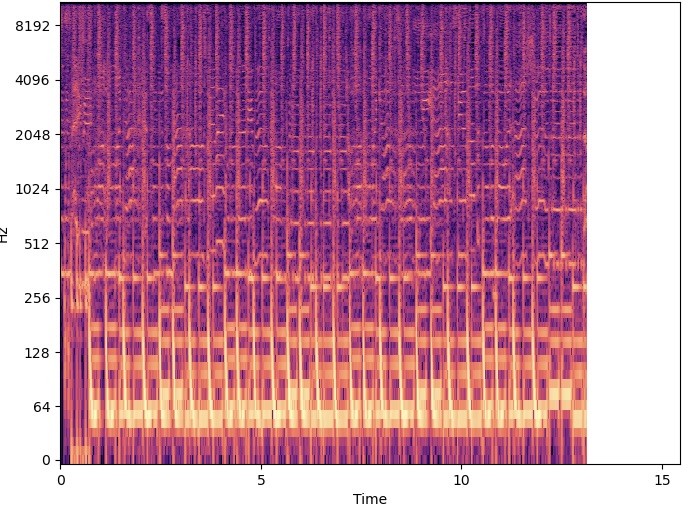
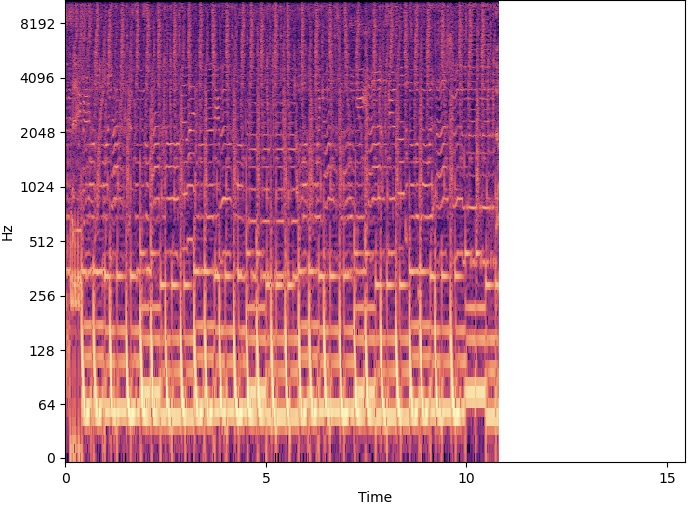
Carving in the Time Domain
| Original | 200 Seams Carved | 400 Seams Carved | |
|---|---|---|---|

|
|
|
Evaluation
As heard above, carving in the frequency domain removed some frequencies that were deemed "unecessary" by the algorithm. When 200 seams were carved in the frequency domain, there was a slight difference but the audio quality was a little lower. When 600 seams were carved in the frequency domain, some of the "ringing" sound from the drums (I'm not sure what instrument") was carved out of the audio. The resulting spectrograms could be seen with slight modifications as well. The axis were static when I created them so the black line of padded zeros cannot be seen that well, but in the 200 seams carved image the seams appear near the top of the spectrogram.
As heard above, carving in the time domain changed the speed in certain spots and shorted the spectrogram image. This specific song has some repetition, and the 200 seams carved audio displays how these sections "sped up" or "were shortened". The algorithm carved out the repetitive parts and kept the non-repetitive parts, and it can be heard how some areas of the song speed up while others stay the same. One thing to note is that there seems to be a limit to how many seams can be cut before the audio playback quality is lost. In the 600 seams carved example, there don't seems to be any artifacts but there is a constant "ringing" sound presumably due to the frequency content being squished together. Nonetheless, the apectrogram plots display the effect of the seam carving algorithm, and how the main content seems to be preserved and the non important content was carved out.
Application
The next goal of mine is to explore the potential of the seam carving algorithm as a data augmentation technique for audio classficiation. Data augmentation has become a critical technique in machine learning to combat the training difficulties that arise from small datasets. The most common model for audio classification are CNNs, and are susceptible to overfitting and data memorization when the data sets are too small. Techniques such as pitch shifting and time scaling alter the audio signal in ways that preserve the original content while introducing variations that decrease model generalization. There is no current research that explores seam carving as a data augmentation technique, so I am working on investigating its possibility.
My main approach has been to take the training and evaluation data and run the seam carving algorithm to carve out a random amount of seams in the frequency domain. I also used librosa's effects pitch shifting to modify the pitch of the audio files by a random number of semitones. This augemented data will serve as the new data and additional data for model training. THe goal is to investigate the effect of the seam carving algorithm in the frequency domain in comparison to another pitch shifting technique.
Currently I am using the dataset from the DCASE 2020 Task 1a challenge dataset and the Resnet models from this github.